StatsNotebook
Causal Mediation Analysis
Tags: Analysis, R code, Regression, Causal Inference
Follow our Facebook page or our developer’s Twitter for more tutorials and future updates.
The tutorial is based on R and StatsNotebook, a graphical interface for R.
Mediation analysis is a technique that examines the intermediate process by which the independent variable affects the dependent variable. For example, family intervention during adolescence (independent variable) can reduce engagement with deviant peer group (mediator) and their experimentation with drugs, which in turn reduces risk of substance use disorder in young adulthood (dependent variable).
StatsNotebook uses the cutting-edge counterfactual framework and Monte Carlo technique to conduct causal mediation analysis. It can handle
- up to 3 mediators;
- numeric, dichotomized and count mediators and dependent variables;
- missing data using multiple imputation.
Since Monte Carlo method is very computationally intensive, it might take a long time to compute the mediation effect. Especially if there are missing data and multiple imputation is used.
Example research questions
- Does reduced engagement with deviant peer groups and reduced experimentation with drugs mediate the effect of the family intervention during adolescence on future substance use disorder?
- In the example, we examine the causal chain “Participation in family intervention -> reduced engagement with deviant peer groups and experimentation with drugs -> substance use disorder in young adulthood”.
- In other words, we expect that participation in family intervention during adolescence reduces engagement with deviant peer groups and experimentation with drugs, which in turns reduces the likelihood for substance use disorder in young adulthood.
In this example, the dependent variable is substance use disorder and the independent variable is family intervention. There are two mediators: engaged with deviant peer group and experimentation with drugs.
We will first show the R codes for this analysis below, and then we will provide a step-by-step guide on how to complete this analysis. We use the built-in substance dataset in this example. This dataset can be loaded into StatsNotebook using the instructions provided here.
In this dataset,
- dev_peer represents engagement with deviant peer groups and it was coded as “0: No” and “1: Yes”;
- sub_exp represents experimentation with drugs and it was coded as “0: No” and “1: Yes”;
- fam_int represents participation in family intervention during adolescence and it was coded as “0: No” and “1: Yes”;
- sub_disorder represents diagnosis of substance use disorder in young adulthood and it was coded as “0: No: and “1: Yes”.
- conflict represents level of family conflict. It will be used as a covariate in this analysis.
This dataset can also be loaded using the following codes
library(tidyverse)
currentDataset <- read_csv("https://statsnotebook.io/blog/data_management/example_data/substance.csv")
R codes
The first section of the code is for imputating missing data. In the second section, we use the mediate function from the intmed package to conduct a mediation analysis.
currentDataset$fam_int_1 = NA
currentDataset$fam_int_1[currentDataset$fam_int == "1"] <- 1
currentDataset$fam_int_1[currentDataset$fam_int == "0"] <- 0
"Multiple imputation"
library(mice)
formulas <- make.formulas(currentDataset)
formulas$gender =gender ~ conflict + sub_disorder + fam_int_1 + dev_peer + sub_exp
formulas$conflict =conflict ~ gender + sub_disorder + fam_int_1 + dev_peer + sub_exp
formulas$sub_disorder =sub_disorder ~ gender + conflict + fam_int_1 + dev_peer + sub_exp
formulas$fam_int_1 =fam_int_1 ~ gender + conflict + sub_disorder + dev_peer + sub_exp
formulas$dev_peer =dev_peer ~ gender + conflict + sub_disorder + fam_int_1 + sub_exp
formulas$sub_exp =sub_exp ~ gender + conflict + sub_disorder + fam_int_1 + dev_peer
meth <- make.method(currentDataset)
imputedDataset <- parlmice(currentDataset,
method = meth,
formulas = formulas,
m = 20,
n.core = 1,
n.imp.core = 20)
plot(imputedDataset)
currentDataset <- complete(imputedDataset, action = "long", include = TRUE)
"Causal Mediation Analysis"
med_res <- intmed::mediate(y = "sub_disorder",
med = c("dev_peer" ,"sub_exp"),
treat = "fam_int_1",
c = c("gender" ,"conflict"),
ymodel = "logistic regression",
mmodel = c("logistic regression" ,"logistic regression"),
treat_lv = 1, control_lv = 0, incint = FALSE, inc_mmint = FALSE,
conf.level = 0.95,
data = currentDataset, sim = 1000, digits = 3,
HTML_report = FALSE, complete_analysis = FALSE,
imputed_data = TRUE)
Using StatsNotebook
Prior to running the causal mediation analysis, we will need to conduct a descriptive analysis and it is always a good practice to visualise the data.
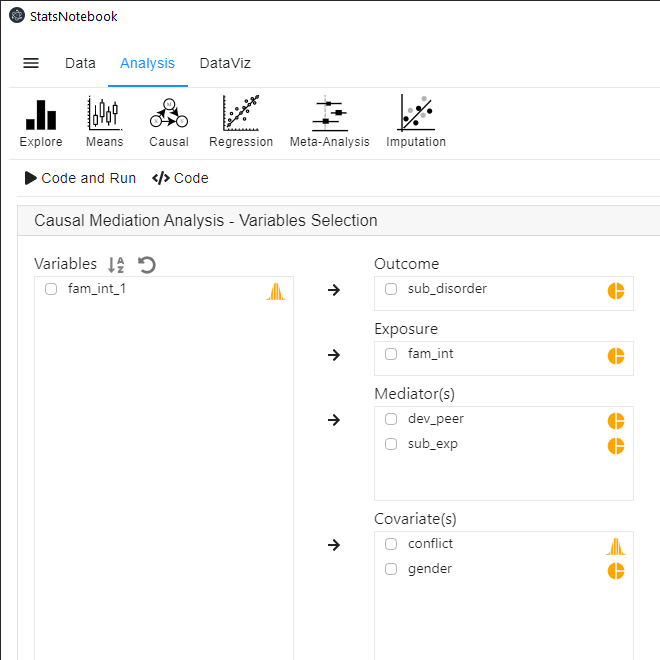
To run a causal mediation analysis,
- Click Analysis at the top
- Click Causal and select Causal Mediation Analysis from the menu
- In the left panel, select sub_disorder into Outcome, fam_int into Exposure, dev_peer and sub_exp into Mediator(s), and gender and conflict into covariates.
- We add gender and conflict as covariates to adjust for their effects.
- All categorical variables will need to be coded as a factor (such as sub_disorder, fam_int, dev_peer, sub_exp and gender. In this example dataset, this has already been done). Converting variable type for step-by-step guide.
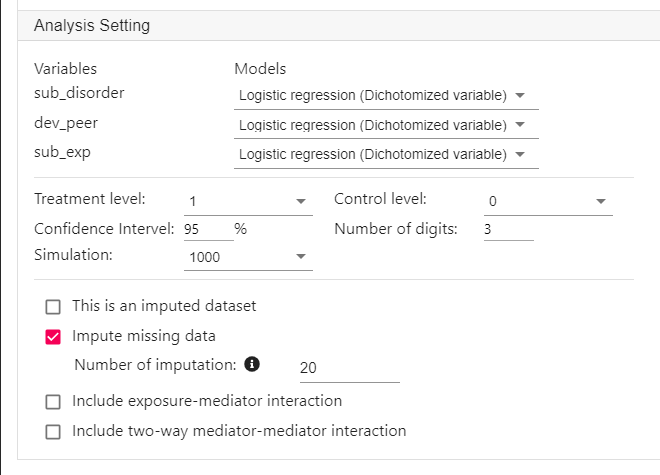
- Expand the panel Analysis Setting.
- Select the models for the mediators and the dependent variable.
- Linear regression for numeric variable
- Logistic regression for dichotomized variable
- Poisson regression for count variable
- In this example, since the mediators and the dependent variable are dichotomized, select Logistic regression (Dichotomized variable) for sub_disorder, dev_peer and sub_exp.
- Select 1 as the treatment level and 0 as the control level.
- If the independent variable is a numeric variable, type 1 for treatment level and 0 for control level.
- Select the 100 as the number of simulations.
- 100 is good for an initial assessment of the mediation effect. For final analysis, use at least 1000 simulations.
- Since there are missing data in this dataset, click Impute missing data, and input 20 as the number of imputations.
- As a rule of thumb, the number of imputations should be around the percentage of missing data.
- Select the models for the mediators and the dependent variable.
Interpretation
Below is the output from StatsNotebook. The analysis is conducted using the intmed package and most of the output is self-explanatory.
There were 25.86% cases with missing data. Multiple imputation was used to impute missing data (Rubin, 2009) and 20 datasets were imputed using the R package MICE (van Buuren, 2010).
The table below shows the estimates from the key regression models for the mediation analysis.
variables m1.b m1.ci m1.p m2.b m2.ci m2.p
1 (Intercept) 0.708 (0.388, 1.292) 0.260 0.980 (0.536, 1.791) 0.947
2 conflict 1.220 (0.963, 1.545) 0.099 1.213 (0.953, 1.544) 0.117
3 genderMale 1.234 (0.861, 1.771) 0.252 1.156 (0.804, 1.661) 0.434
4 fam_int_1 0.517*** (0.358, 0.747) 0.000 0.539** (0.369, 0.788) 0.001
5 dev_peer1 <NA> <NA> <NA> <NA> <NA> <NA>
6 sub_exp1 <NA> <NA> <NA> <NA> <NA> <NA>
y.b y.ci y.p
1 0.061*** (0.019, 0.200) 0.000
2 0.820 (0.531, 1.267) 0.371
3 1.396 (0.779, 2.501) 0.262
4 0.603 (0.331, 1.102) 0.100
5 4.132*** (1.891, 9.031) 0.000
6 1.745 (0.739, 4.123) 0.203
Mediation analysis was performed based on the counter-factual framework and the interventional effect (Vansteelandt and Daniel, 2017; Chan and Leung, 2020). The analysis was conducted in R using the intmed package (Chan and Leung, 2020) with 1000 simulations.
effect est ci
1 indirect effect through mediator 1 -0.018 (-0.037, -0.004)
2 indirect effect through mediator 2 -0.007 (-0.021, 0.004)
3 indirect effect through interaction between mediators 0.001 (-0.002, 0.005)
4 indirect effect through dependence between mediators 0.000 (-0.009, 0.009)
5 direct effect -0.055 (-0.120, 0.010)
6 total effect -0.077 (-0.143, -0.016)
7 proportion of effect through mediator 1 0.218
8 proportion of effect through mediator 2 0.078
p
1 0.005
2 0.202
3 0.448
4 0.975
5 0.099
6 0.011
7
8
Reference
Rubin DB. Multiple imputation for nonresponse in surveys. New York: John Wiley & Sons; 2009.
Buuren Sv, Groothuis-Oudshoorn K. mice: Multivariate imputation by chained equations in R. Journal of statistical software. 2010:1-68.
Vansteelandt S, Daniel RM. Interventional effects for mediation analysis with multiple mediators. Epidemiology (Cambridge, Mass). 2017; 28(2):258.
Chan G, Leung J. Causal mediation analysis using the interventional effect approach. A refined definition. Paper uner review. 2020.
There are two key sections of the output: Results from regression models and Results from mediation analysis.
Results from regression models
Behind the scene, three key regression models are run.
- dev_peer (mediator) is regressed on fam_int (independent variable), gender and conflict in a logistic regression
- This is to assess the effect of fam_int on dev_peer, adjusting for gender and conflict.
- sub_exp (mediator) is regressed on fam_int (independent variable), gender and conflict in a logsitic regression
- This is to assess the effect of fam_int on dev_peer, adjusting for gender and conflict
- sub_disorder (dependent variable) is regressed on dev_peer (mediator), sub_exp (mediator), fam_int (indenpendent variable), gender and conflict in a logistic regression.
- This is to assess the effect of dev_peer, sub_exp and fam_int on sub_disorder, adjusting for gender and conflict.
The table below from the StatsNotebook summarises the odds ratio, 95% confidence intervals and p-value from these three models. With a significance level of 0.05, the results indicate that participation in family intervention reduces the odds of engagement with deviant peers, OR = 0.517, 95% CI (0.358, 0.747) and experimentation with drugs, OR = 0.539, 95% CI (0.369, 0.788). Family intervention may reduce odds of substance use disorder directly, OR = 0.603, 95% CI (0.331, 1.102), but this effect is not statistically significant. Engagement with deviant peers increased the odds of substance use disorder, OR = 4.132, 95% CI (1.891, 9.031). Experimentation with drugs may increase the odds of substance use disorder, OR = 1.745, 95% CI (0.739, 4.123), but this effect is not statistically significant.
The table below shows the estimates from the key regression models for the mediation analysis.
variables m1.b m1.ci m1.p m2.b m2.ci m2.p
1 (Intercept) 0.708 (0.388, 1.292) 0.260 0.980 (0.536, 1.791) 0.947
2 conflict 1.220 (0.963, 1.545) 0.099 1.213 (0.953, 1.544) 0.117
3 genderMale 1.234 (0.861, 1.771) 0.252 1.156 (0.804, 1.661) 0.434
4 fam_int_1 0.517*** (0.358, 0.747) 0.000 0.539** (0.369, 0.788) 0.001
5 dev_peer1 <NA> <NA> <NA> <NA> <NA> <NA>
6 sub_exp1 <NA> <NA> <NA> <NA> <NA> <NA>
y.b y.ci y.p
1 0.061*** (0.019, 0.200) 0.000
2 0.820 (0.531, 1.267) 0.371
3 1.396 (0.779, 2.501) 0.262
4 0.603 (0.331, 1.102) 0.100
5 4.132*** (1.891, 9.031) 0.000
6 1.745 (0.739, 4.123) 0.203
Results from mediation analysis
The second table shows the results from mediation analysis.
Mediation analysis was performed based on the counter-factual framework and the interventional effect (Vansteelandt and Daniel, 2017; Chan and Leung, 2020). The analysis was conducted in R using the intmed package (Chan and Leung, 2020) with 1000 simulations.
effect est ci
1 indirect effect through mediator 1 -0.018 (-0.037, -0.004)
2 indirect effect through mediator 2 -0.007 (-0.021, 0.004)
3 indirect effect through interaction between mediators 0.001 (-0.002, 0.005)
4 indirect effect through dependence between mediators 0.000 (-0.009, 0.009)
5 direct effect -0.055 (-0.120, 0.010)
6 total effect -0.077 (-0.143, -0.016)
7 proportion of effect through mediator 1 0.218
8 proportion of effect through mediator 2 0.078
p
1 0.005
2 0.202
3 0.448
4 0.975
5 0.099
6 0.011
7
8
Since sub_disorder is a dichotomised variable, the estimates are in a probability scale. Overall, the total effect of fam_int is -0.077, indicating that participation in family intervention reduces the probability of sub_disorder by 0.077 (i.e. 7.7%). Of this total effect, 0.018 (est = -0.018, 95% CI [-0.037, -0.004]) is significantly mediated through dev_peer and 0.007 (est = -0.007, 95% CI [-0.021, 0.004]) is mediated through sub_exp. Overall, it is estimated that 21.8% of the total effect is mediated through dev_peer and 7.8% through sub_exp.
Follow our Facebook page or our developer’s Twitter for more tutorials and future updates.